并查集

概述

并查集是一种树性的数据结构，主要用于解决一些集合的合并，查询的问题。比如将多个元素合并到一个集合里；查询两个元素是否属于同一个集合。

实际运用：(看题就知道了)

547. 省份数量 - 力扣（Leetcode）

399. 除法求值 - 力扣（Leetcode）

684. 冗余连接 - 力扣（Leetcode）

工作原理

基本原理

先用一个数组来存储元素，数组的索引代表元素，值存储着该元素的父亲的下标。如果两个元素的老祖宗是一样的，那么这两个元素属于同一个集合。

初始情况：

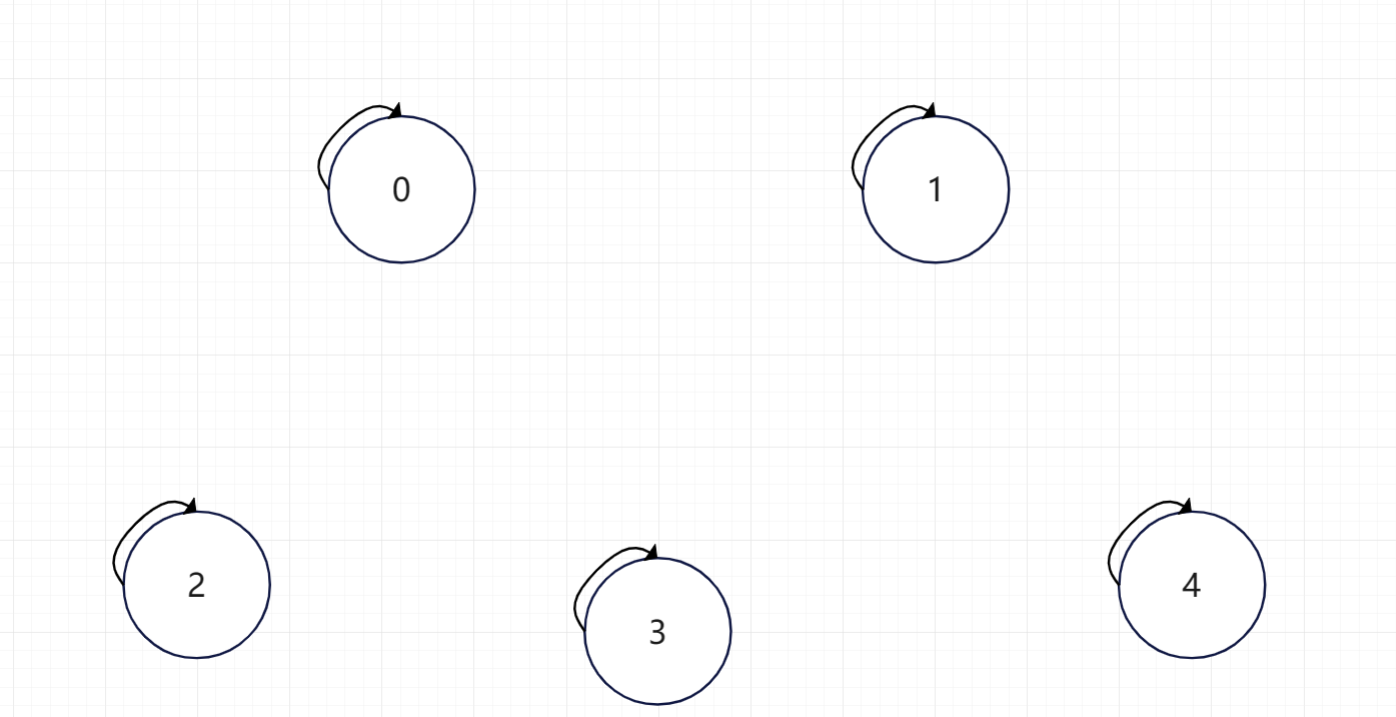
image-20221223155802818

初始情况，所有人的父亲都指向自己，也意味这自己属于一个集合。

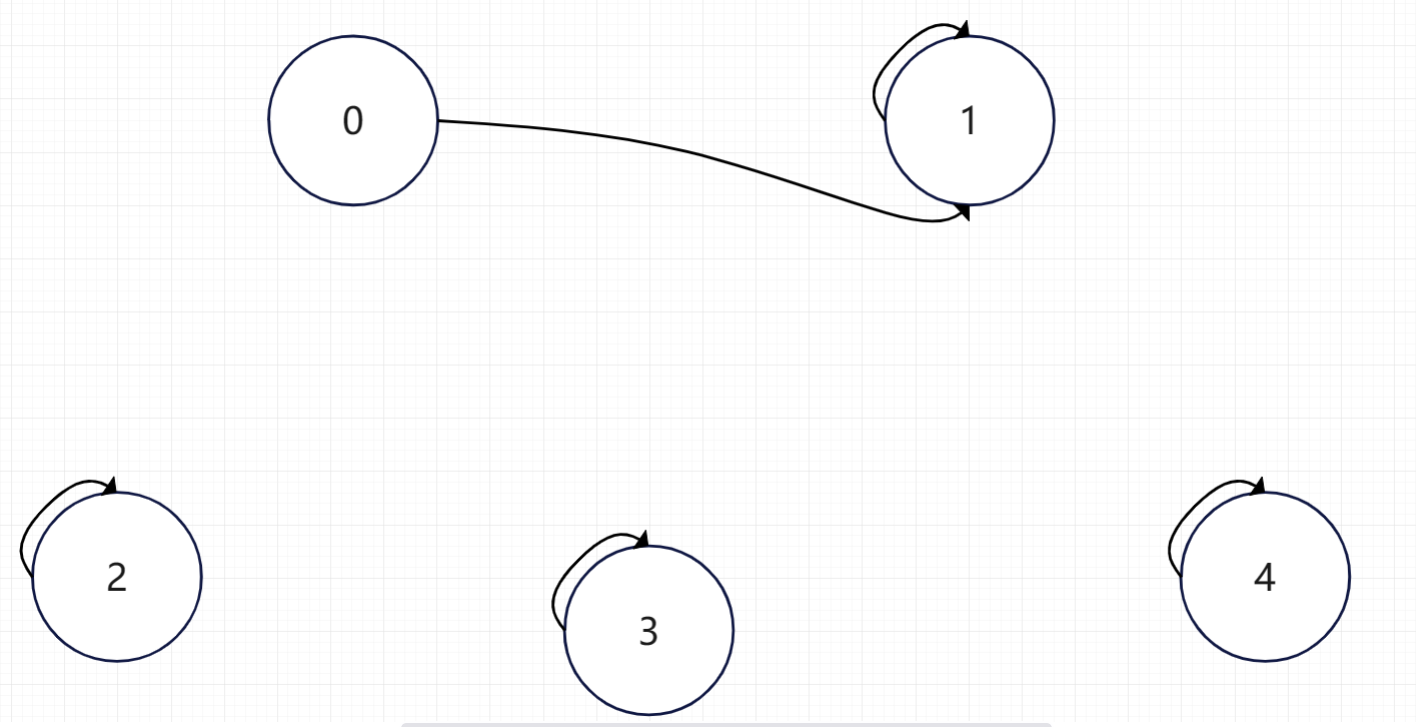
image-20221223155916294

现在，我们0所在集合归并到1所在集合中去。只需要让0的父亲指向1即可。即让0认1做爹，然后他们就属于一个家族了。

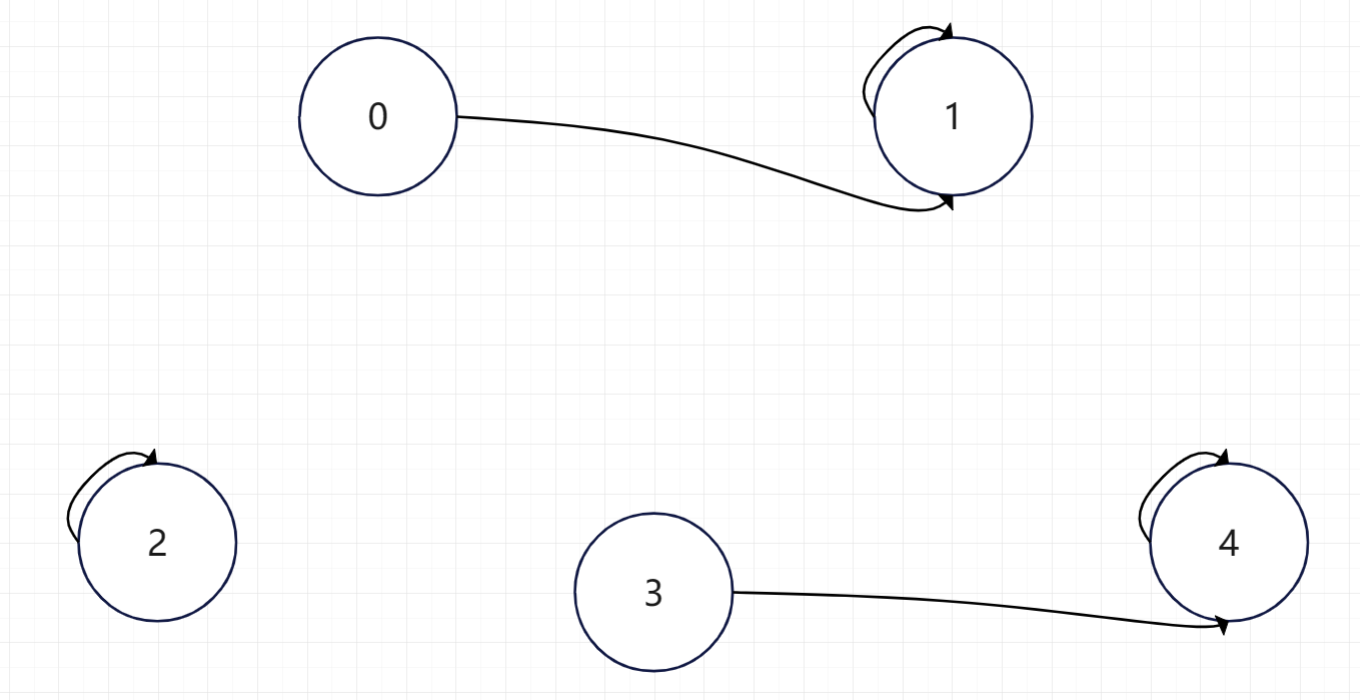
image-20221223160003818

假如我们现在又想让3所在集合合并到4所在集合。那么只需要将3的父亲指向4即可。即让3认4做爹，然后他们就属于一个家族了。

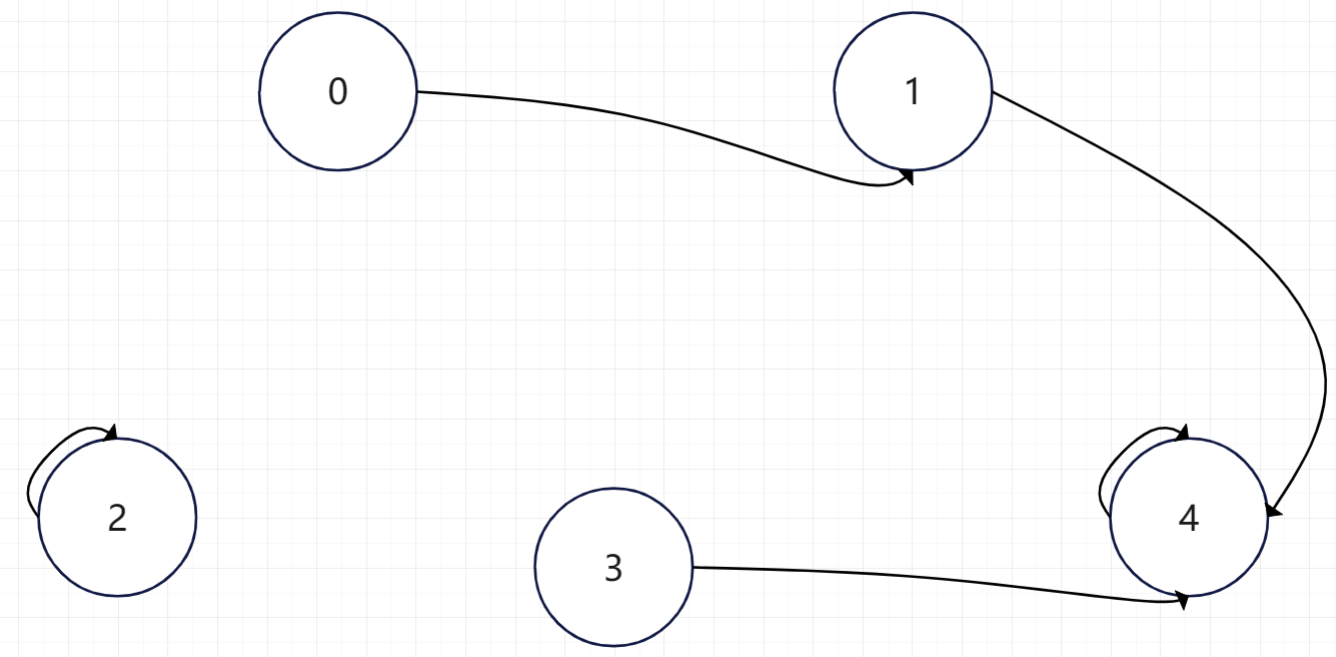
image-20221223160054090

假如，我们现在又想让0所在家族合并到3所在家族。那么我们只需要让0的父亲指向3的父亲即可。即让0的父亲认3的父亲做爹。那么他们就都属于一个家族了。（我们这里一定让0的父亲认3的父亲做爹才能合并成一个更大的家族，如果只是让0去认3的父亲做爹的话，那么0的父亲就会被孤立出来，不在这个家族里）

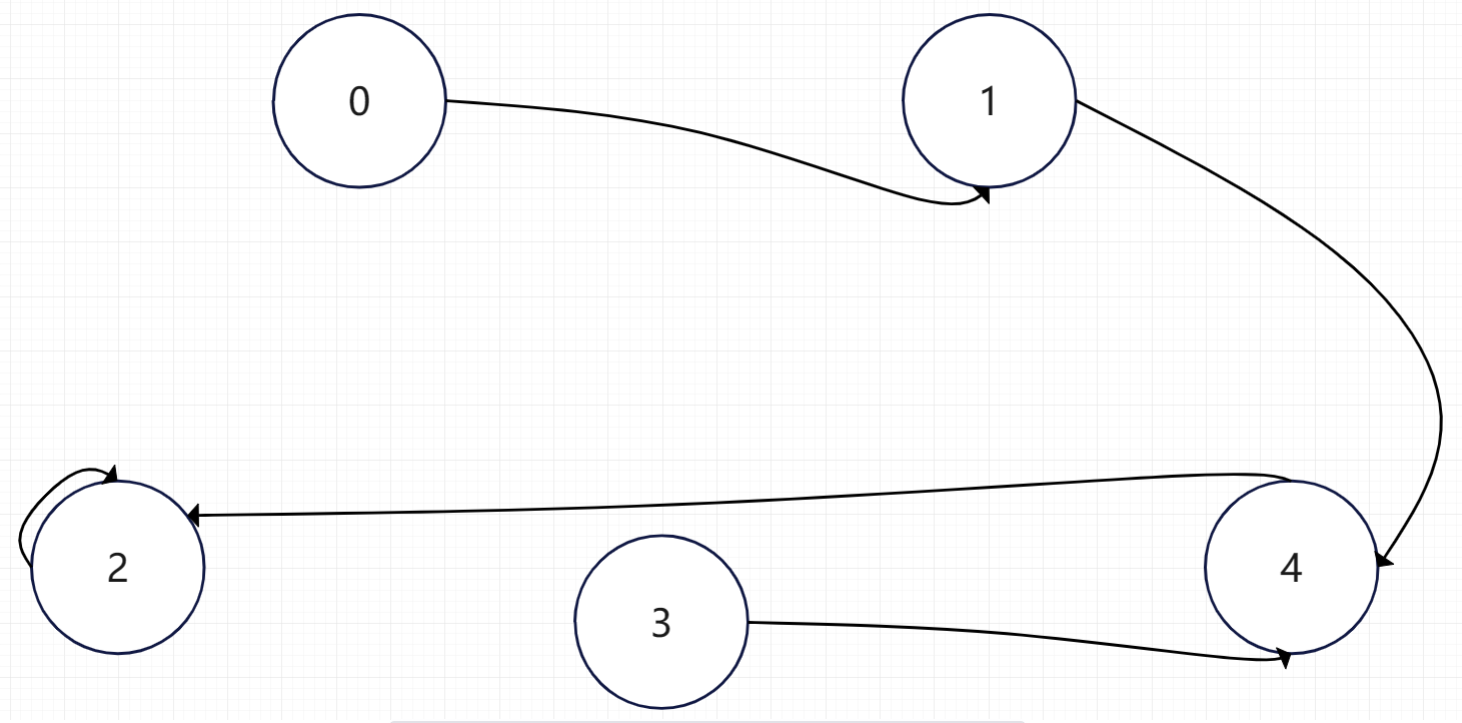
image-20221223160128387

我们继续让0所在集合合并到2所在集合中去。我们只需要让0的祖宗指向2即可。即让0的老祖宗认2做爹，然后他们就是一个更大的家族了。

如果我们要要判断两个元素是否属于一个集合，只需要去判断两个元素是否有同一个祖宗即可。比如这里，1的祖宗是2，3的祖宗也是2，所以1和3属于同一个集合。

特别申明：这里的祖宗和认爹行为纯粹是我用来搞笑的，并非专业术语。

路径压缩

image-20221223160128387

对于该图，我们每次要去寻找一个节点的祖宗的时候，需要不停的遍历父亲节点。我们可以使用路径压缩，让其直接指向自己的祖宗节点。

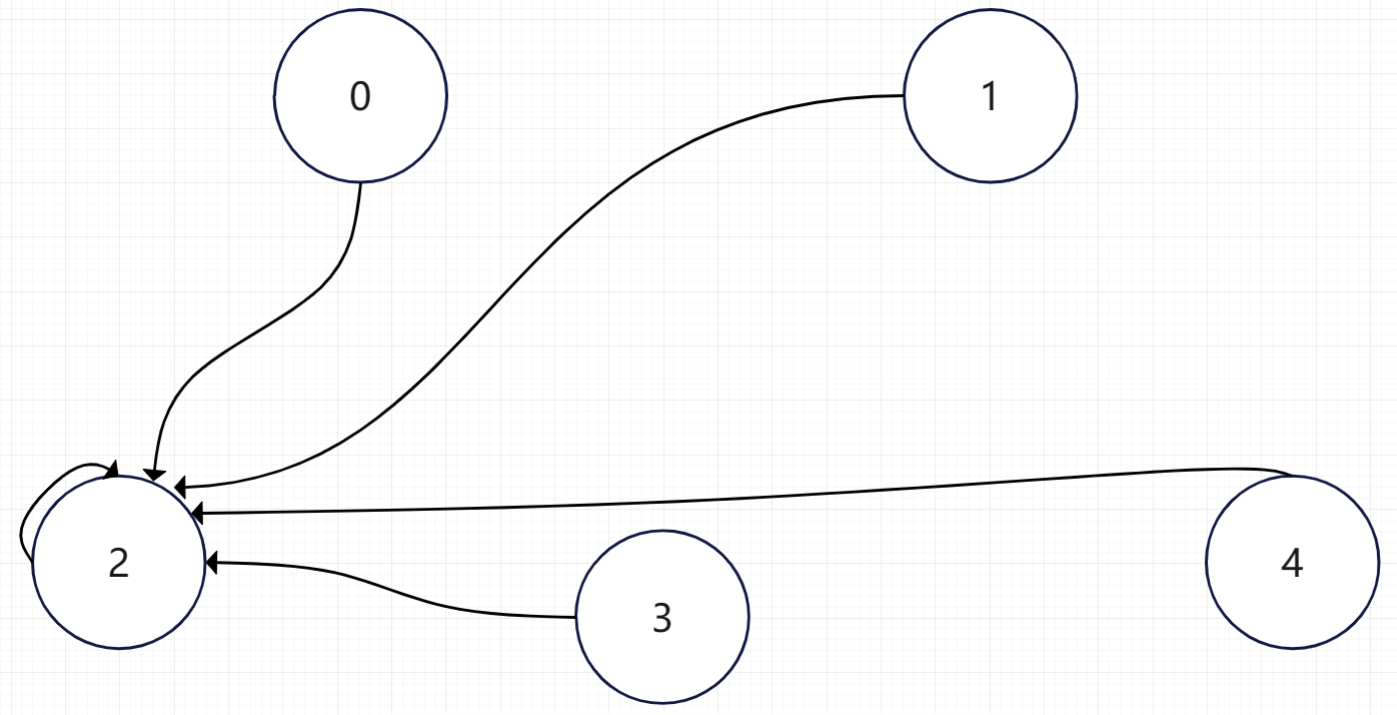
image-20221223160242038

这样就不需要一个个遍历了，具体如何实现路径压缩，看代码比较好理解。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class UnionSet {
    // 集合数目
    public int count;
    // 存储当前下标的父亲
    private int[] parent;

    public UnionSet(int size) {
        this.count = size;
        this.parent = new int[size];
        // 起始情况，让所有的元素的父亲指向自己
        for (int i = 0; i < size; i++) {
            this.parent[i] = i;
        }
    }

    // 查找x元素的祖宗
    // 使用了路径压缩
    public int find(int x) {
        if (parent[x] == x) {
            return x;
        }
        int p = find(parent[x]);
        parent[x] = p;
        return p;
    }

    // 未使用路径压缩
    public int find2(int x) {
        if (parent[x] == x) {
            return x;
        }
        return find(parent[x]);
    }

    // x所在集合和并到y所在集合
    public void union(int x, int y) {
        int p1 = find(x);
        int p2 = find(y);
        if (p1 == p2) {
            return;
        }
        //将两个集合合并成一个集合，则集合数目减1
        count--;
        parent[p1] = p2;
    }

    // 判断x和y是否属于同一个集合
    public boolean isConnection(int x, int y){
        return find(x) == find(y);
    }
    
    // 获取集合数目
    public int getCount() {
        return this.count;
    }
}