前缀和

一维前缀和

前缀和可以用来求数组中0 到 i 的所有数字之和。对于数组a，如果我们要创建一个数组，里面存储的是 a[0] 到 a[i] 的所有数字之和。我们只需要遍历 a, 令 a[i] = a[i] + a[i - 1]即可。

1
2
3
4
5
6
7
8
class Solution {
    public int[] preSum(int[] a) {
        for (int i = 1; i < a.length; i++) {
            a[i] += a[i - 1];
        }
        return a;
    }
}

例题

560. 和为 K 的子数组 - 力扣（Leetcode）

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的连续子数组的个数 。

示例 1：

1
2
输入：nums = [1,1,1], k = 2
输出：2

示例 2：

1
2
输入：nums = [1,2,3], k = 3
输出：2

其他例题
525. 连续数组 - 力扣（Leetcode）
724. 寻找数组的中心下标 - 力扣（Leetcode）

解答

  • 先求出nums的前缀和a。 a[i] 表示了 nums[0] 到 nums[i] 所有数字之和，其中 a[j] - a[i] 就等于 nums[i + 1] 到 nums[j] 之和。我们只需要两次遍历 a ，如果a[j] - a[j] == k ，则个数加一。
  • 对于该题，我们可以使用hash进行一个优化，key为前缀和，value为该前缀和出现的数目
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int subarraySum(int[] nums, int k) {
        int sum = 0;
        Map<Integer, Integer> map = new HashMap<>(nums.length);
        map.put(0,1);
        int answer = 0;
        for (int num : nums) {
            sum += num;
            if (map.containsKey(sum - k)) {
                answer += map.get(sum - k);
            } 
            if (map.containsKey(sum)) {
                map.put(sum, map.get(sum) + 1);
            } else {
                map.put(sum, 1);
            }
        }
        return answer;
    }
}

二维前缀和

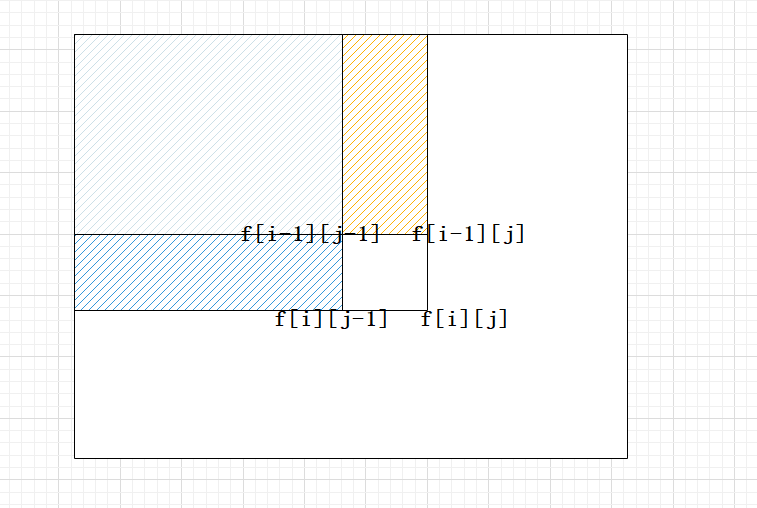
对于二维前缀和，其实就是一个二维数组的前缀和。假设 f 为二维数组 a 的前缀和数组。那么 f[ i ] [ j ] 就是 a[0] [0] 到a[i] [j]所形成的矩阵的所有数之和。

23424224edfs

具体做法：f[i] [j] = f[i - 1] [j] + f[i] [j - 1] - f[i - 1] [j - 1] + a[i] [j]

image-20230118002852579

例题

304. 二维区域和检索 - 矩阵不可变 - 力扣（Leetcode）

给定一个二维矩阵 matrix，以下类型的多个请求：

  • 计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。

实现 NumMatrix 类：

  • NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
  • int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。

示例 1：

img

1
2
3
4
5
6
7
8
9
10
11
输入: 
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出: 
[null, 8, 11, 12]

解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

其他例题
1738. 找出第 K 大的异或坐标值

解答

  • 这个很明显就是二维前缀和，我们只需要维护一个二维前缀和数组 f 就行。假设我们需要求 (row1, col1) 到 （row2, col2) 所表示的长方形面积，只需要：s = f[row2] [col2] - f[row1 -1] [col2] - f[row2] [col1 - 1] + f[row1 - 1] f[col - 1] 即可。
  • 下面题解的二维前缀和数组创建得比原数组长1。目的是为了避免一些边界的判断。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class NumMatrix {
    // 二维前缀和数组
    private int[][] presum;
    public NumMatrix(int[][] matrix) {
        // 求二维前缀和
        presum = new int[matrix.length + 1][matrix[0].length + 1];
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                presum[i + 1][j + 1] = presum[i][j + 1] + presum[i + 1][j] - presum[i][j] + matrix[i][j];
            }
        }
        this.presum = presum;
    }
    
    public int sumRegion(int row1, int col1, int row2, int col2) {
        return presum[row2 + 1][col2 + 1] - presum[row1][col2 + 1] - presum[row2 + 1][col1] + presum[row1][col1];
    }
}

差分

一维差分

差分有点类似于前缀和，大家都知道前缀和是计算前n个数之和的，a[i] = a[i] + a[i-1]。而差分则是记录“相邻两个数之差”。a[i] = a[i] - a[i - 1]，即可求出差分数组。

  • 对于一个数组的差分，我们只需要对差分数组进行一遍前缀和即可求出原数组

例题

1094. 拼车 - 力扣（Leetcode）

车上最初有 capacity 个空座位。车 只能 向一个方向行驶（也就是说，不允许掉头或改变方向）

给定整数 capacity 和一个数组 trips , trip[i] = [numPassengersi, fromi, toi] 表示第 i 次旅行有 numPassengersi 乘客，接他们和放他们的位置分别是 fromi 和 toi 。这些位置是从汽车的初始位置向东的公里数。

当且仅当你可以在所有给定的行程中接送所有乘客时，返回 true，否则请返回 false。

示例 1：

1
2
输入：trips = [[2,1,5],[3,3,7]], capacity = 4
输出：false

示例 2：

1
2
输入：trips = [[2,1,5],[3,3,7]], capacity = 5
输出：true

其它例题
1109. 航班预订统计 - 力扣（Leetcode）

解答

  • 差分数组有一个很重要的特性，即差分数组的前缀和数组就是原数组。这还可以推导出一个有趣的点。假设差分数组中b[i] = c, 那么在原数组中，i 索引以后的所有数都会加上 c。
  • 对于上题中，我们可以用一个数组 a 来存储一路上的乘客数目。我们只需要遍历 trip 然后在 a 数组的 fromi 到 toi - 1索引位置上都加上 numPassengersi 就可以计算出一路上各个位置需要搭乘的乘客数量。不过显然在这题上过于暴力，会超时
  • 其实我们只需要创建另一个数组，t ，让t[ fromi ] 的位置加上 numPassengersi，让t[ toi - 1] 的位置减去 numPassengeri。然后计算 t 的前缀和，t 的前缀和就是数组a。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public boolean carPooling(int[][] trips, int capacity) {
        //获取差分数组的应该预留的长度
        int len = 0;
        for (int[] trip : trips) {
            if (trip[2] > len) {
                len = trip[2];
            }
        }
        int[] a = new int[len + 1];
        // 构建差分数组
        for (int[] trip : trips) {
            a[trip[1]] += trip[0];
            a[trip[2]] -= trip[0];
            
        }
        // 求前缀和
        for (int i = 0; i < a.length; i++) {
            if (i > 0){
                a[i] += a[i - 1];
            }
            if (a[i] > capacity) {
                return false;
            }
        }
        return true;
    }
}

二维差分

例题

2536. 子矩阵元素加 1 - 力扣（Leetcode）

给你一个正整数 n ，表示最初有一个 n x n 、下标从 0 开始的整数矩阵 mat ，矩阵中填满了 0 。

另给你一个二维整数数组 query 。针对每个查询 query[i] = [row1i, col1i, row2i, col2i] ，请你执行下述操作：

  • 找出 左上角 为 (row1i, col1i) 且 右下角 为 (row2i, col2i) 的子矩阵，将子矩阵中的 每个元素 加 1 。也就是给所有满足 row1i <= x <= row2i 和 col1i <= y <= col2i 的 mat[x][y] 加 1 。

返回执行完所有操作后得到的矩阵 mat 。

示例 1：

img

1
2
3
4
5
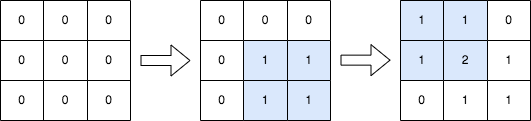
输入：n = 3, queries = [[1,1,2,2],[0,0,1,1]]
输出：[[1,1,0],[1,2,1],[0,1,1]]
解释：上图所展示的分别是：初始矩阵、执行完第一个操作后的矩阵、执行完第二个操作后的矩阵。
- 第一个操作：将左上角为 (1, 1) 且右下角为 (2, 2) 的子矩阵中的每个元素加 1 。 
- 第二个操作：将左上角为 (0, 0) 且右下角为 (1, 1) 的子矩阵中的每个元素加 1 。

示例 2：

img

1
2
3
4
输入：n = 2, queries = [[0,0,1,1]]
输出：[[1,1],[1,1]]
解释：上图所展示的分别是：初始矩阵、执行完第一个操作后的矩阵。 
- 第一个操作：将矩阵中的每个元素加 1 。

解答

  • 显然这个是一个二维差分的题目。类似于一维差分。我们需要求出二维差分数组，然后对二维差分数组求前缀和，即可得到答案。

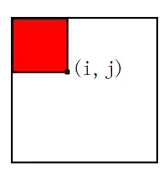
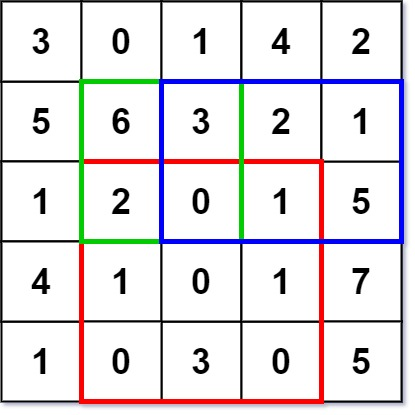
  • 先给出结论，我们构建差分数组的时候，如果要在（row1, col1) 到 (row2, col2) 所组成的矩阵中的所有位置都加一。那么我们在差分数组中的 (row1, col1)位置+1，在(row2 + 1, col2 + 1)位置+1，在(row1, col2 + 1)位置-1，在(row2 + 1, col)位置-1，得到差分数组。如下图：

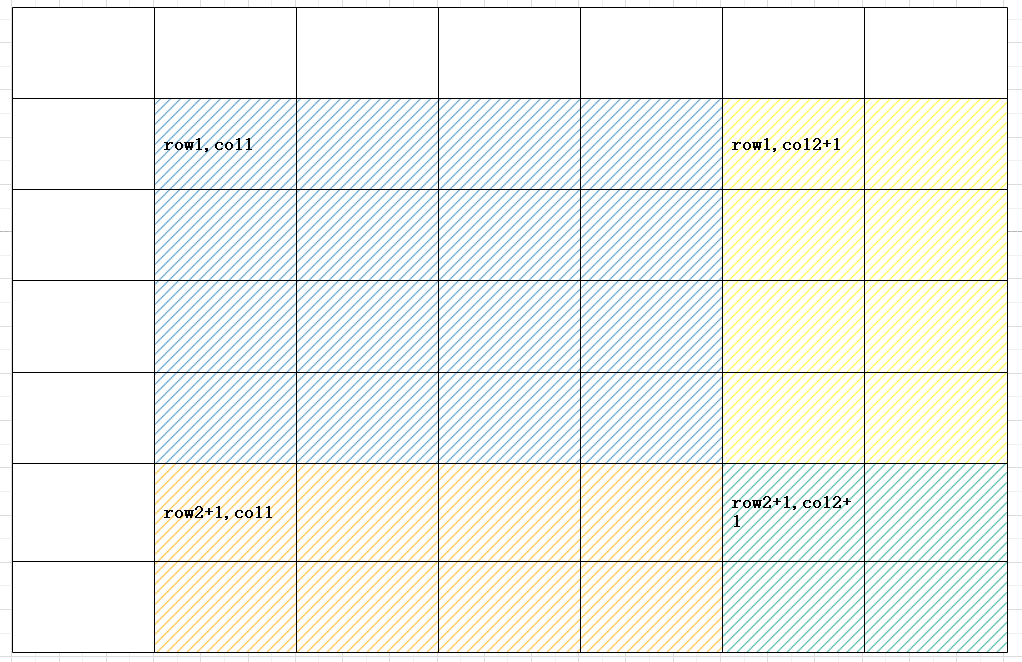
    image-20230118112546041

  • 我们需要在求前缀和数组的时候，蓝色长方形中所有格子都+1。

  • 我们在差分数组中(row1,col1)位置+1，求其前缀和数组，row1,col1的右下边所有格子都会+1。但是我们只需要在(row1,col1)到(row2,col2)所形成的数组中+1即可。

  • 所以需要在(row2+1,col1)位置-1，保证橘色部分的时候不受row1,col1的影象。加一减一中和掉了。

  • 在(row1, col2+1)位置-1，保证黄色部分不受row1,col1的影响。加一减一中和掉了。

  • 在(row2+1,col2+1)位置+1，在绿色部分，的前缀和都会加上(row1,col1)、(row1,col2+1)、（row2+1,col1)、(row2+1,col2+1)。由于两次加一，两次减一，最终结果为0，绿色部分也不受影响。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int[][] rangeAddQueries(int n, int[][] queries) {
        int[][] t = new int[n + 1][n + 1];
        //构建差分数组
        for (int[] q : queries) {
            int row1 = q[0];
            int col1 = q[1];
            int row2 = q[2];
            int col2 = q[3];
            t[row1][col1]++;
            t[row2+1][col1]--;
            t[row1][col2+1]--;
            t[row2+1][col2+1]++;
            
        }
        //求前缀和
        int[][] answer = new int[n + 1][n + 1];
        for (int i = 1; i < answer.length; i++) {
            for (int j = 1; j < answer[0].length; j++) {
                answer[i][j] = answer[i-1][j] + answer[i][j-1] - answer[i-1][j-1] + t[i-1][j-1];
            }
        }
        answer = Arrays.copyOfRange(answer, 1, n + 1);
        for (int i = 0; i < answer.length; i++) {
            answer[i] = Arrays.copyOfRange(answer[i], 1, n+1);
        }
        return answer;
    }
}