欧拉回路

介绍

• 七桥问题

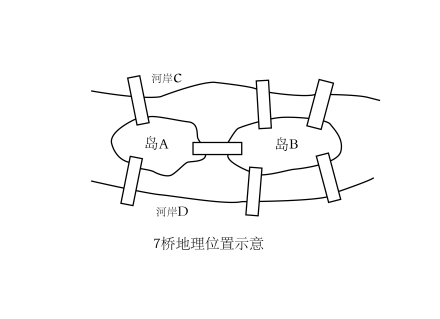
18世纪初普鲁士的哥尼斯堡，有一条河穿过，河上有两个小岛，有七座桥把两个岛与河岸联系起来（如图）。有个人提出一个问题：一个步行者怎样才能不重复、不遗漏地一次走完七座桥，最后回到出发点。这就是所谓的七桥问题

后来大数学家欧拉把它转化成一个几何问题【一笔画问题】，并解决了该问题。思路就是把岸，岛，想象成一个点。把桥想象成一个边。

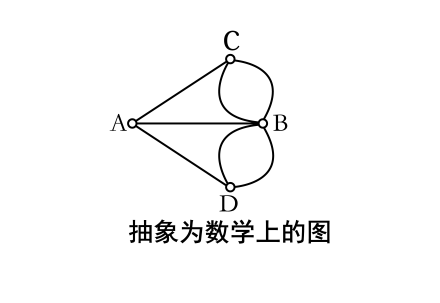
这样，七桥问题就转换成了，如何一笔走过图中的所有路径。

• 一些定义

对于一个图的一条路径，可以经过所有的边，且只通过一次，那么这个路径就称为欧拉路径。

对于一个图的一条路径，可以经过所有的边，且只通过一次，并能回到出发点，那么这个路径也称为欧拉回路

对于一个图，如果含有欧拉回路，则称这个图为欧拉图

对于一个图，如果含有欧拉路径而无欧拉回路，则称这个图为半欧拉图

判断是否存在欧拉回路

对于无向图

结论：

如果一个图所有的顶点所连接的边都是偶数，那么该图存在欧拉回路。如果含有顶点连接的边数为奇数，那么该图不存在欧拉回路。

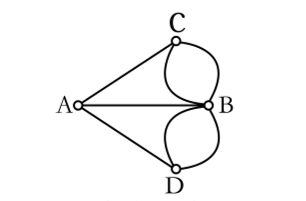
对于这图，点A，B，C，D所连接的的边都是奇数，所以并不存在欧拉回路。及七桥问题的答案就是不存在一条这样的路径。

如何理解：为何相连顶点如果是奇数，则一定没有欧拉回路

一个顶点有奇数条相连的边意味着，有至少有一次经过该顶点是只进不出，或者只出不进的。

• 如果该顶点是起始顶点，则最后一次从起始顶点出发，只能出，不能进，无法回到起始顶点。
• 如果该顶点是非起始顶点，则最后一次经过该顶点，只能进不能出，只能在非起始顶点结束，无法回到起始顶点。

对于有向图

如果一个图所有的顶点的出度等于入度，那么该图存在欧拉回路。如果出度不等于入度，那么该图不存在欧拉回路。

理解和无向图类似。

Hierholzer 算法

该算法用于找到一个欧拉图/半欧拉图中的欧拉回路/欧拉路径

半欧拉图找欧拉路径

步骤

• step 1: 选择一个合适的开始node(这个合适的node其实是欧拉路径/欧拉回路的起始点)

  • 对于无向图, 为一个度数为奇数的顶点(如果所有点的度数为偶数则随机一点);
  • 对于有向图, 为一个出度比入度多1的顶点(如果均相同则为随机一点).

• step 2: 从node开始进行深度优先遍历, 对于当前点, 枚举其相邻的顶点, 并删除该边, 递归到相邻顶点(配合代码理解比较直观), 如果与当前顶点相连的所有边都已经被遍历, 将该点加入到队列中, 进行回溯

• step 3: 队列中存储着反向欧拉路径/回路.

下面是一道leetcode题目

332. 重新安排行程 - 力扣（Leetcode）

class Solution {
    private Map<String, PriorityQueue<String>> map;
    private Stack<String> stack;

    public List<String> findItinerary(List<List<String>> tickets) {
        map = new HashMap<>();
        stack = new Stack<>();
        //把边添加到map
        for (List<String> ticket : tickets) {
            PriorityQueue<String> nexts = map.getOrDefault(ticket.get(0), new PriorityQueue<>());
            nexts.add(ticket.get(1));
            map.put(ticket.get(0), nexts);
        }
        dfs("JFK");
        //读取欧拉路径
        List<String> answer = new ArrayList<>();
        while (stack.size() != 0) {
            answer.add(stack.pop());
        }
        return answer;
    }
    
    private void dfs(String curr) {
        while (map.containsKey(curr) && map.get(curr).size() != 0) {
            String next = map.get(curr).poll();
            dfs(next);
        }
        stack.push(curr);
    }
}