检验图中是否有环

判断图中是否有环一共有三种方法：

拓扑排序
DFS
并查集

下面所有代码都是实现一个方法：

class Solution {
    //检验图中是否有环，edges用来存储边，[2,3]表示2节点到3节点有一条有向或无向边
    //该图是一个连通图
    // n为节点数目
    // 节点的标识在[0,n)之间
    public boolean isLoop(int[][] edges,int n) {
    }
}

拓扑排序

有向图

过程

对于有向图，循环遍历图中所有入度为0的顶点并去除，直到最终没有顶点可以去除。如果还有顶点剩下，则剩下的就是环路。如果没有顶点剩下，则不存在环。

假如有一个有向图

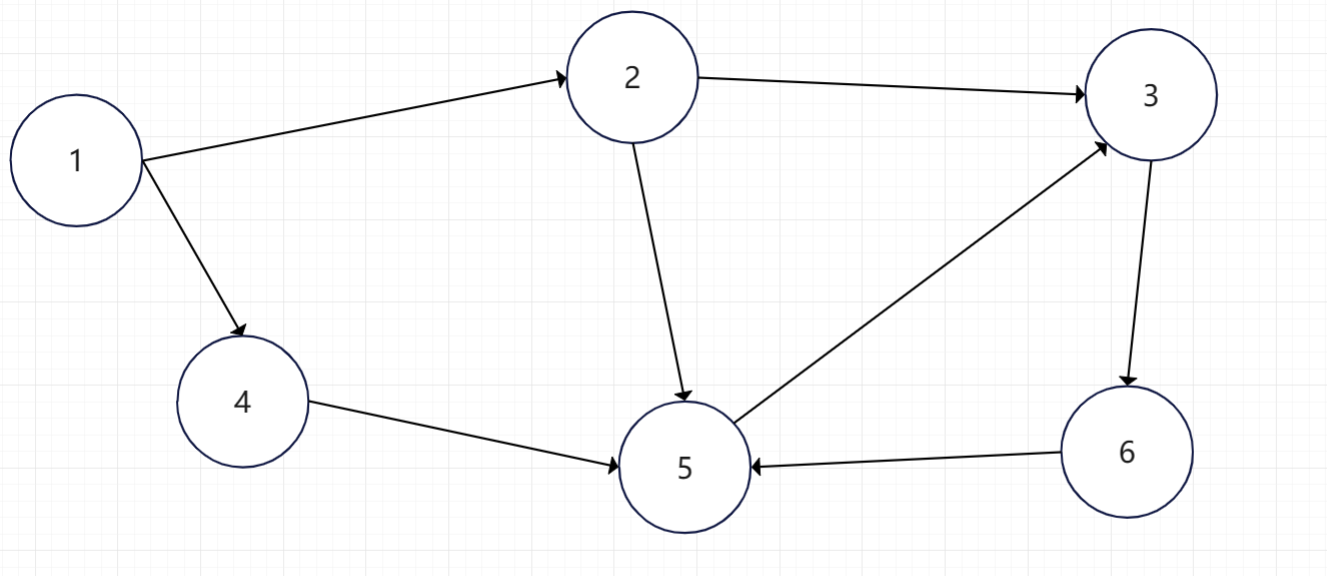
入度为0的顶点有1顶点，则第一步先去除1顶点

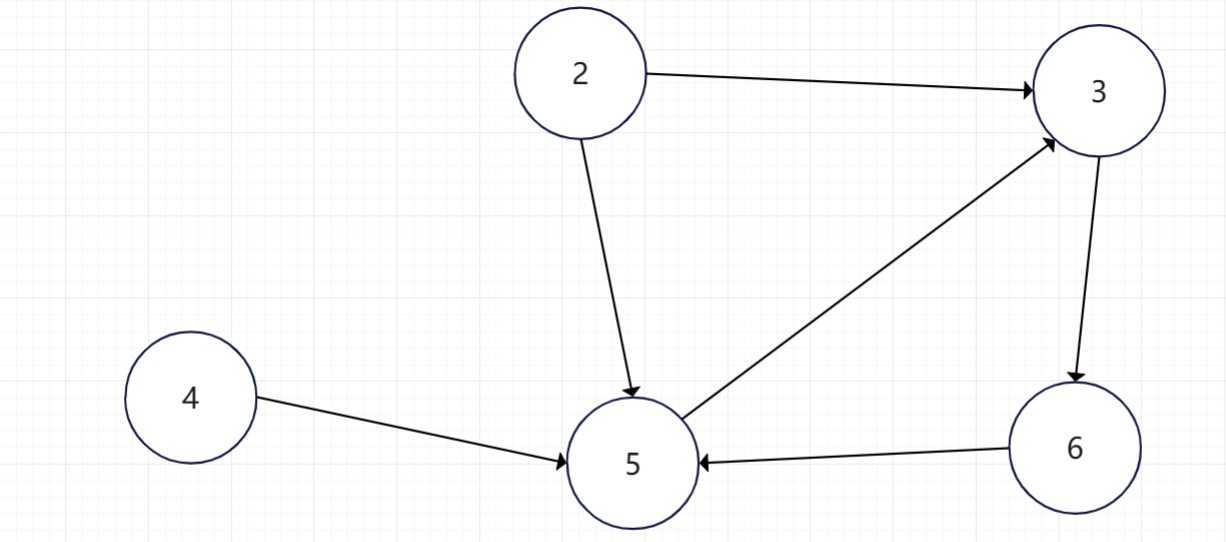
现在入度为0的顶点有4顶点和2顶点，依次去除4顶点和2顶点

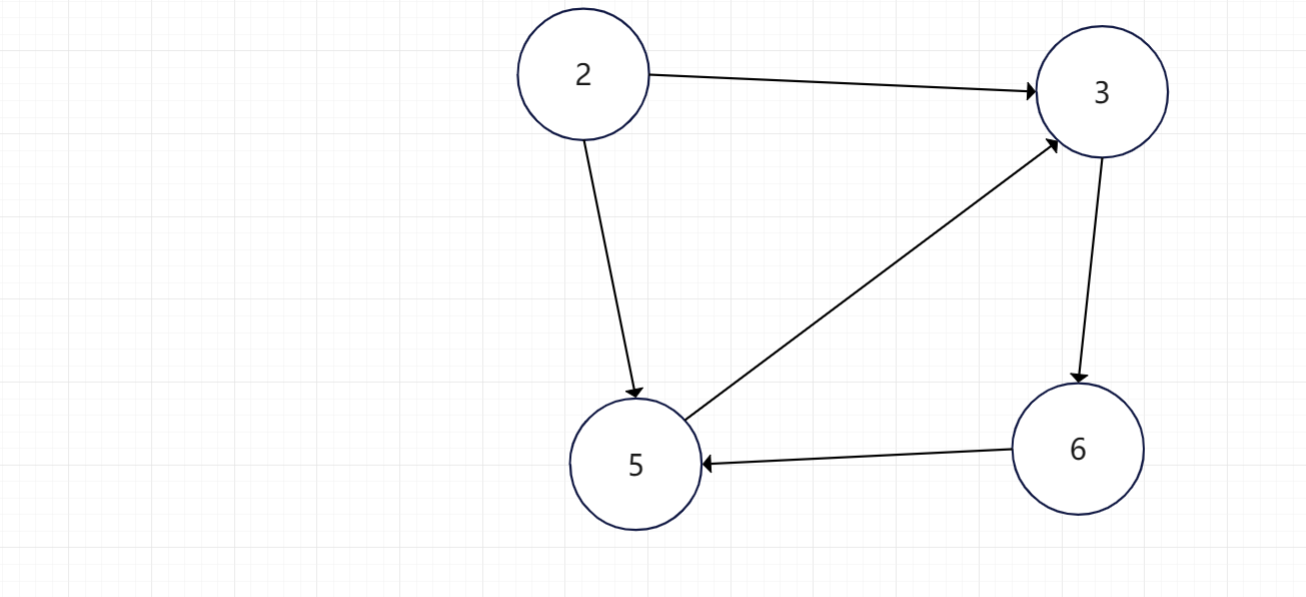
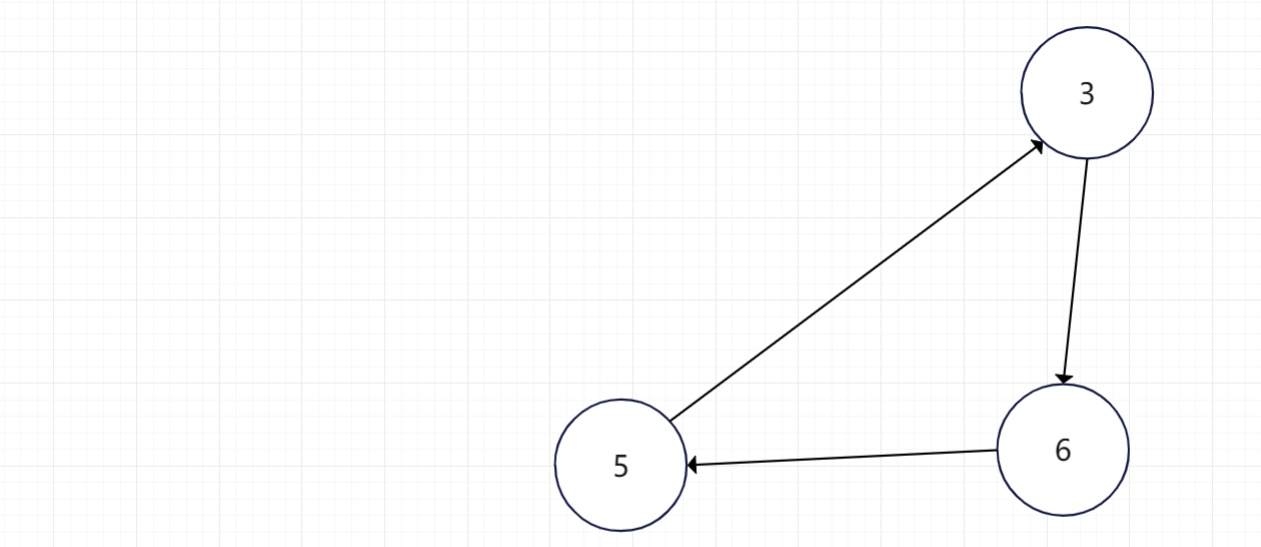
没有可去除的顶点了，该图有环路，顶点3、5、6形成环

代码实现

class Solution {
    // 拓扑排序算法
    public boolean isLoop(int[][] edges, int n) {
        //记录边
        List<List<Integer>> edgeList = new ArrayList<>();
        //记录入度
        int[] deg = new int[n];
        for (int i = 0; i < n; i++) {
            edgeList.add(new ArrayList<>());
        }
        for (int[] edge : edges) {
            // 添加到到edgeMap
            edgeList.get(edge[0]).add(edge[1]);
            // 记录入度
            deg[edge[1]]++;
        }
        //第一次获取入度为0的点
        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < deg.length; i++) {
            if (deg[i] == 0) {
                queue.offer(i);
            }
        }
        int removeCount = 0;
        while (queue.size() != 0)  {
            int node = queue.poll();
            removeCount++;
            List<Integer> nextNodes = edgeList.get(node);
            // 在图中去除节点node，并让所有的nextNodes的入度-1
            for (Integer nextNode : nextNodes) {
                deg[nextNode]--;
                // 如果发现nextNode度数为0添加到队列，等待去除
                if (deg[nextNode] == 0) {
                    queue.add(nextNode);
                }
            }
        }
        // 如果移除节点数目不是节点总数，则有环
        return removeCount != deg.length;
    }
}

无向图

过程

对于无向图，循环遍历图中所有度数小于1的顶点并去除，直到最终没有顶点可以去除。如果还有顶点剩下，则剩下的就是环路。如果没有顶点剩下，则不存在环。

假如有个无向图

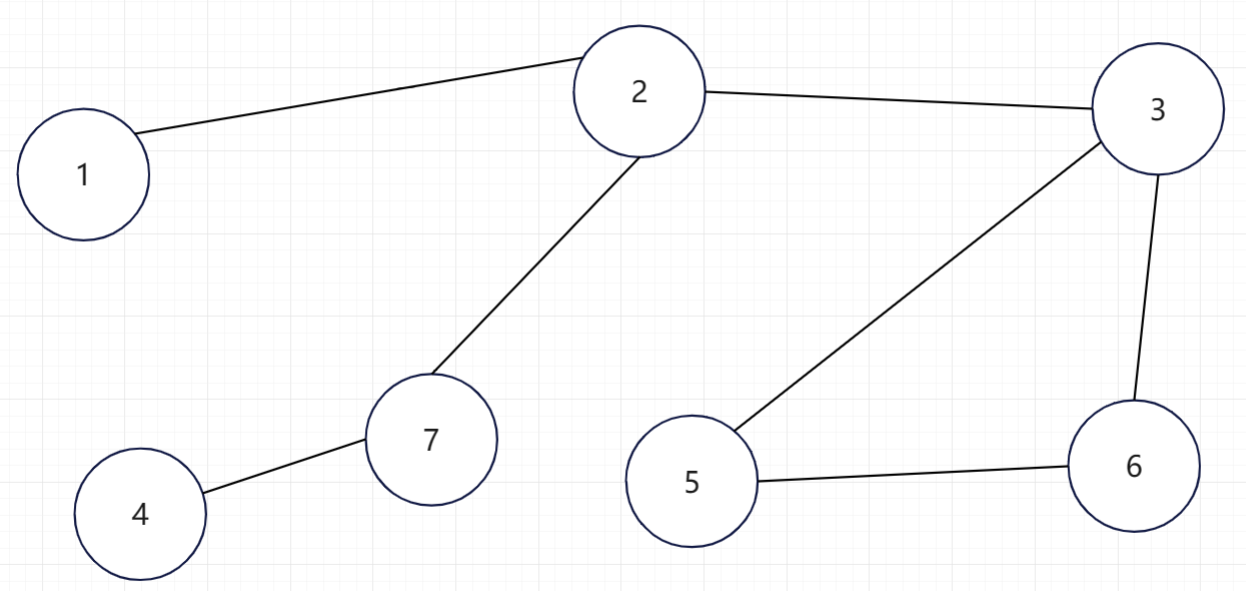
找到度数为1的顶点分别是顶点1和顶点4，依次去除

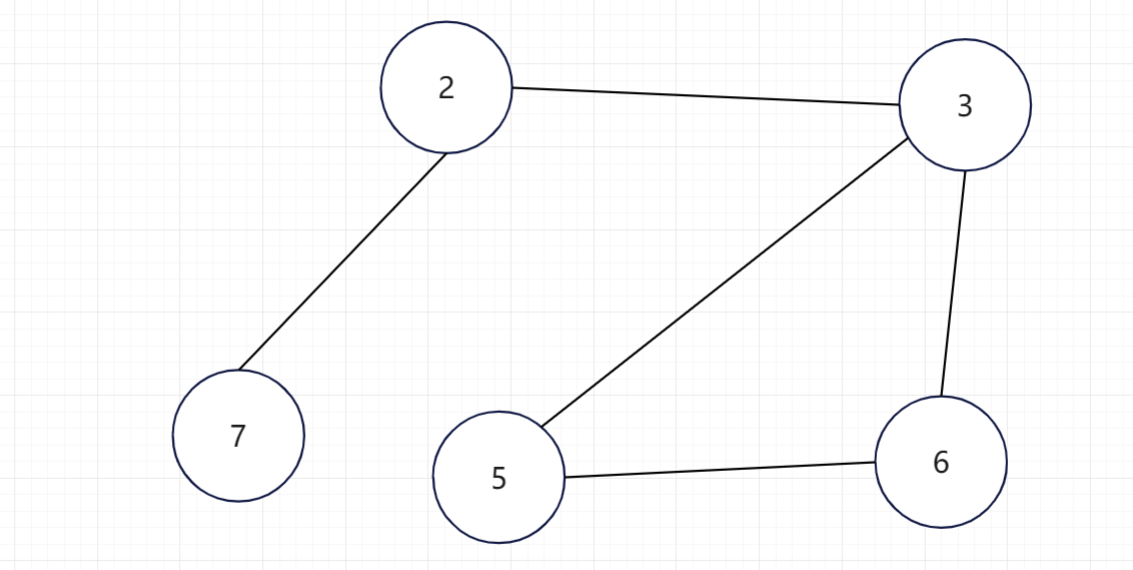
继续找入度为1的顶点为顶点7，去除顶点7

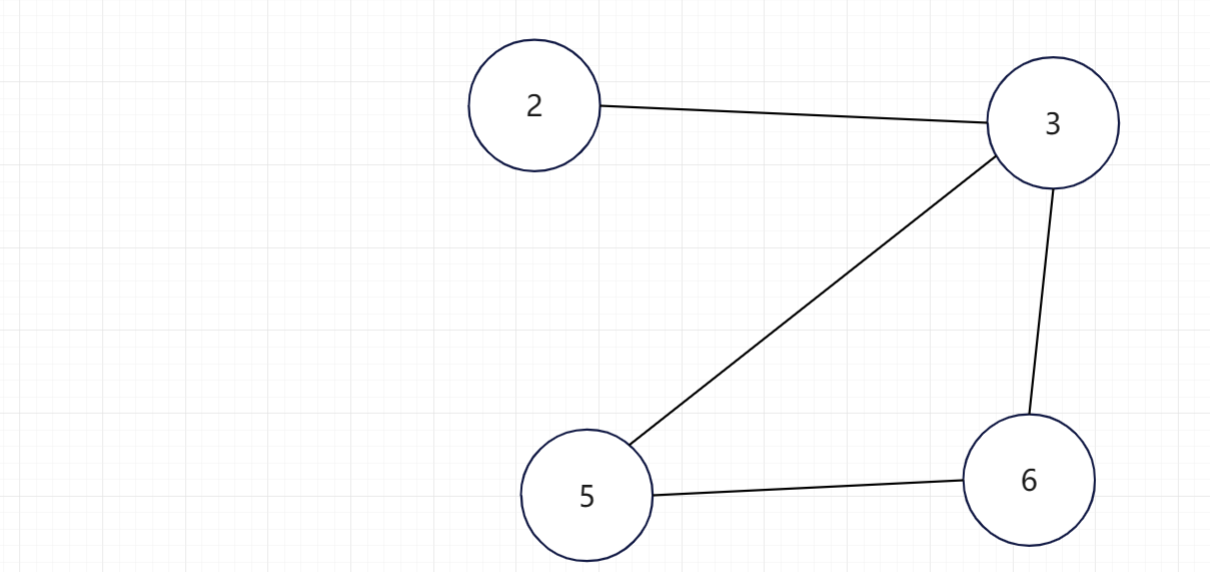
继续找度数为1的顶点，找到顶点2，去除顶点2

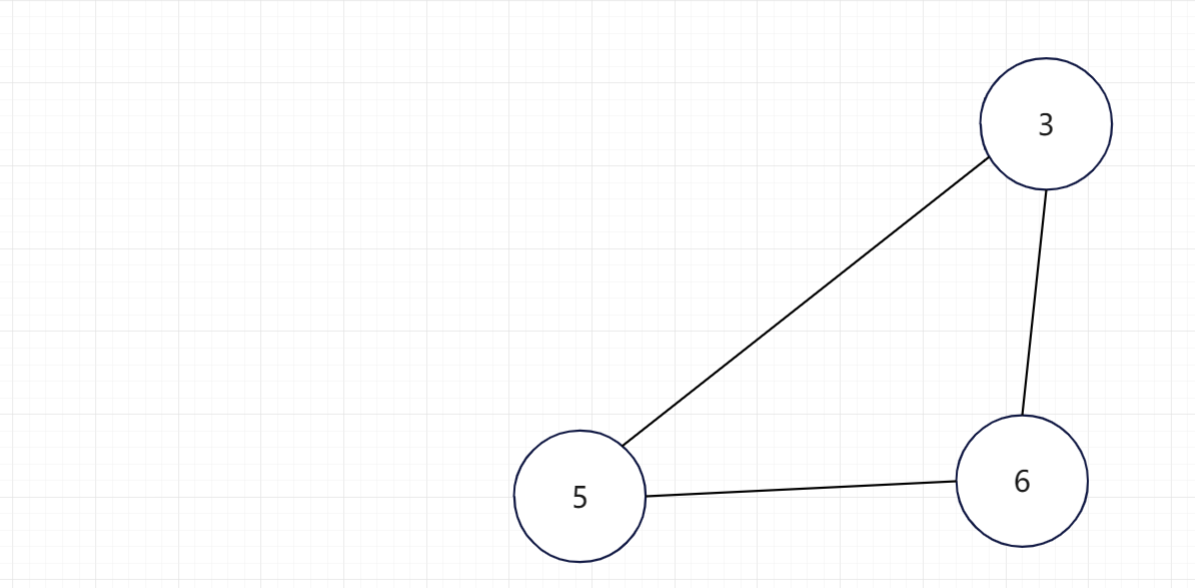
无法继续删除顶点，出现环路

代码实现

参考有向图，实现类似

DFS

有向图和无向图思路都差不多，深度优先遍历，如果发现有一个顶点重新遍历了，则说明出现环路。

有向图

class Solution {
    //保存边
    List<List<Integer>> edgeList;
    //检验一个节点是否被遍历过，0代表没有遍历过，1代表在此次深度优先中遍历过，2代表过去遍历过
    int[] visited;
    boolean answer = false;
    public boolean isLoop(int[][] edges,int n) {
        edgeList = new ArrayList<>();
        visited = new int[n];
        for (int i = 0; i < n; i++){
            edgeList.add(new ArrayList<>());
        }
        for (int[] edge : edges) {
            edgeList.get(edge[0]).add(edge[1]);
        }
        //进行遍历
        for (int node = 0; node < n; node++) {
            if (visited[node] == 0){
                dfs(node);
            }
            if (answer){
                return true;
            }
        }
        return false;
    }

    private void dfs(int node) {
        // 如果当前节点已被遍历过退出dfs
        if (visited[node] == 1) {
            answer = true;
            return;
        }
        visited[node] = 1;
        List<Integer> nextNodes = edgeList.get(node);
        for (Integer nextNode : nextNodes) {
            dfs(nextNode);
            // 出现环路则不需要继续遍历，返回即可
            if (answer) {
                return;
            }
        }
        visited[node] = 2;
    }
}

无向图

与有向图类似

并查集

如果不了解并查集可以看这一篇博客

并查集 | 逆流的博客 (fansqz.com)

无向图

过程

使用并查集去解决无向图环路问题。其实可以理解为找出一条多余的边。对于一个含有n个顶点的图，我们可以通过n-1条边将其相连起来，多出的边将导致环路。对于并查集我们可以理解为，我们根据边将两个顶点合并到一集合中去，如果发现这两个顶点本身就处于一个集合中，则这条边会导致环路。具体步骤如下：

遍历所有边<i,j>，判断顶点 i 是否和 j 处于一个集合
如果不属于一个集合，则调用union(i,j)合并到一个集合
如果本身就属于一个集合，则出现环路，并退出循环

代码实现

class Solution {
    public boolean isLoop(int[][] edges,int n) {
        UnionSet unionSet = new UnionSet(n);
        for (int[] edge : edges) {
            if (!unionSet.union(edge[0], edge[1])){
                return false;
            }
        }
        return true;
    }
}

class UnionSet {
    private int[] parent;

    public UnionSet(int size) {
        this.parent = new int[size];
        for (int i = 0; i < size; i++){
            this.parent[i] = i;
        }
    }

    public boolean union(int x, int y) {
        int p1 = find(x);
        int p2 = find(y);
        if (p1 == p2) {
            return false;
        }
        parent[p1] = p2;
        return true;
    }

    public int find(int x) {
        if (parent[x] == x) {
            return x;
        }
        int p = find(parent[x]);
        parent[x] = p;
        return p;
    }
}