最短路径

介绍

一个顶点到另一个顶点的最短的距离，叫最短路径。

Dijkstra(迪杰斯特拉)

Dijkstra 算法是求一个图中一个点到其他所有点的最短路径的算法，基于「贪心」、「广度优先搜索」、「动态规划」，时间复杂度是O(n2)

用文字比较难描述，下面用图来讲。目标：找到顶点 0 到所有顶点的最小距离

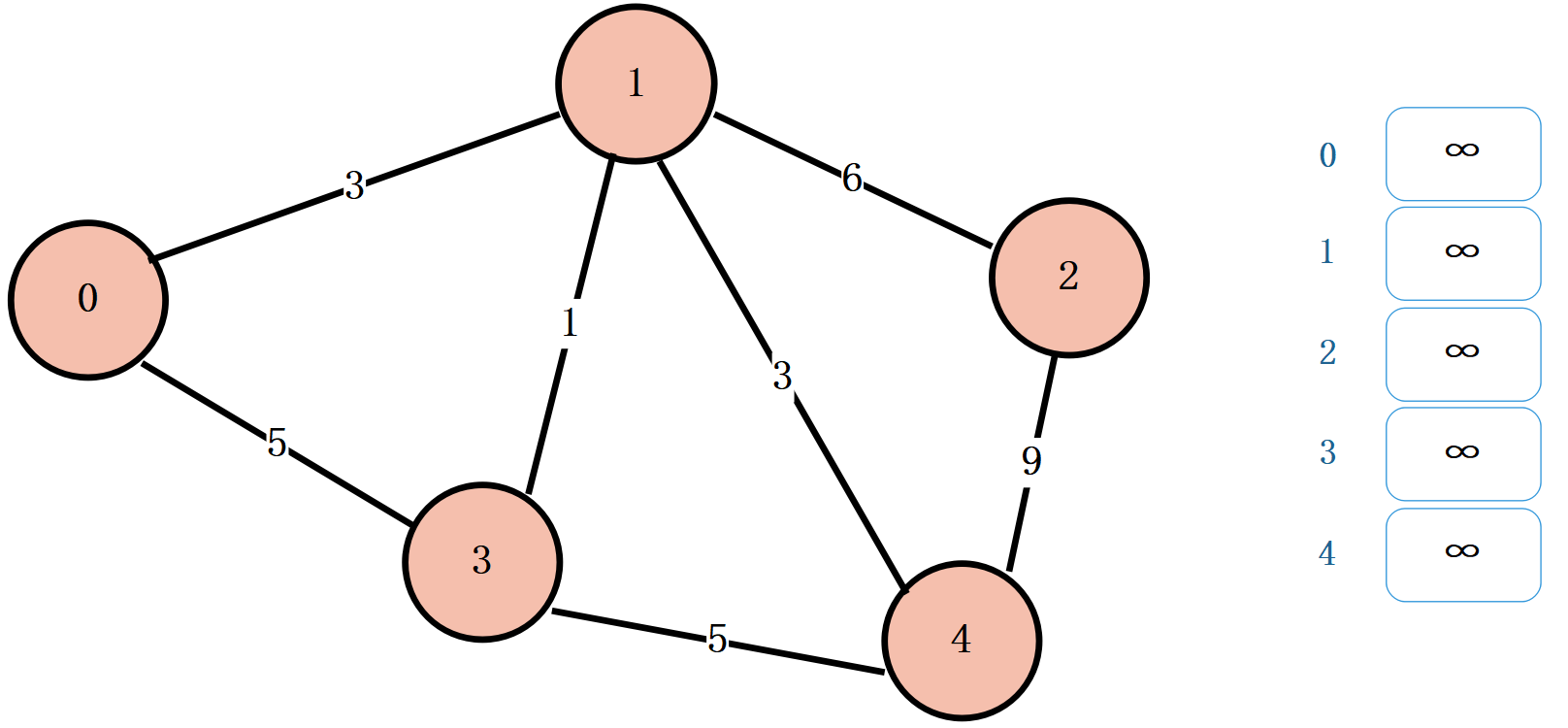
首先我们需要一个数组来记录起始顶点到所有顶点的距离。初始情况，先将所有距离设置为无穷

image-20221230201109899

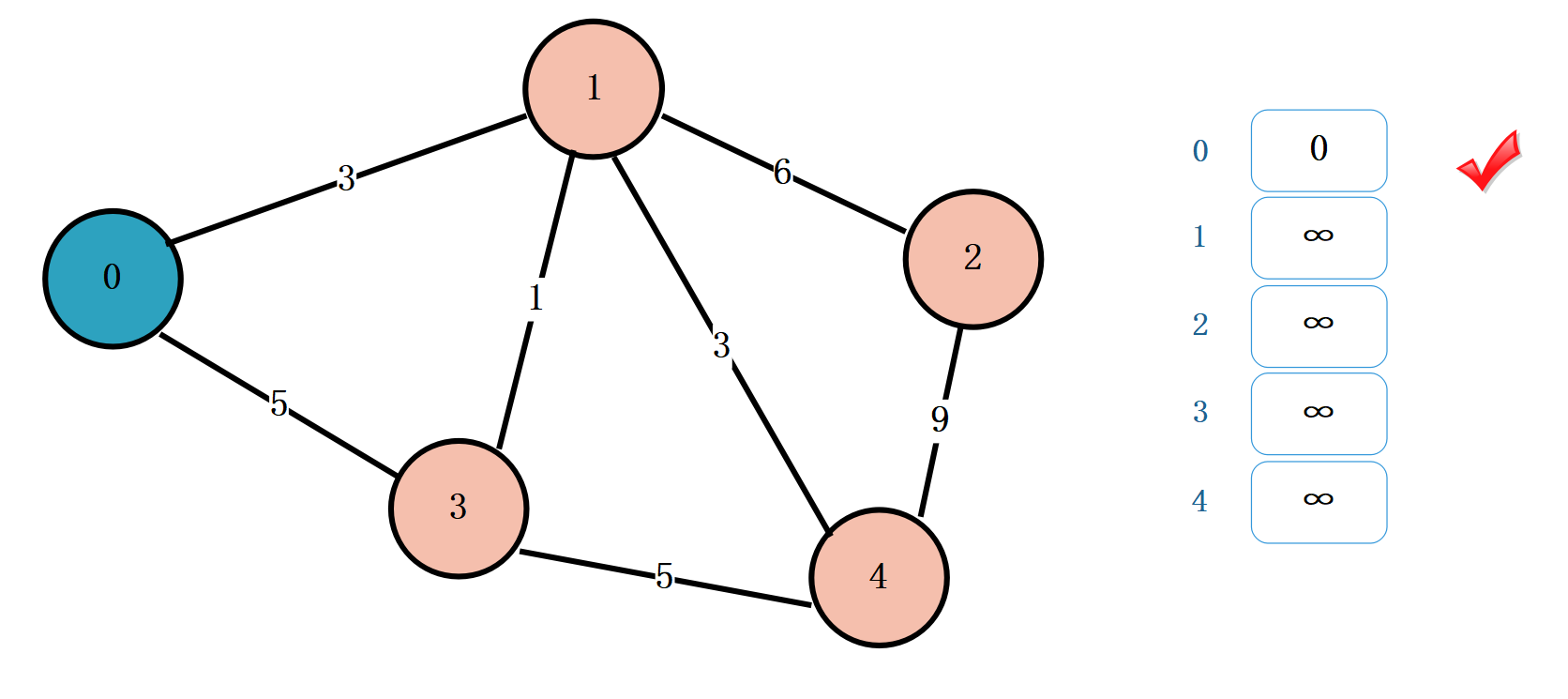
更新顶点 0 到顶点 0 的距离为 0。标记顶点 0 ，设置 0 为顶点 0 到顶点 0 的最小距离

image-20221230203705506

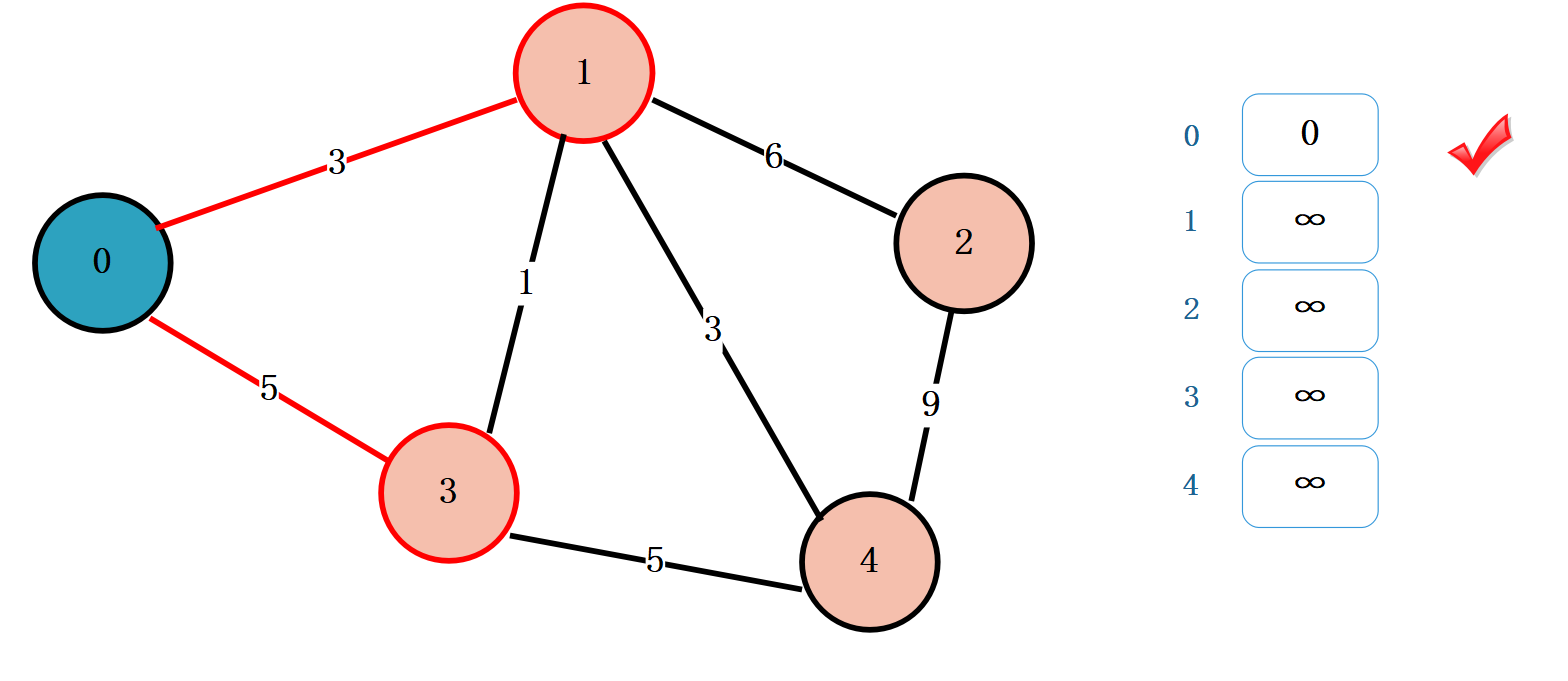
从顶点 0 出发，找到相邻的未被标记的顶点为 1、3。

image-20221230203808790

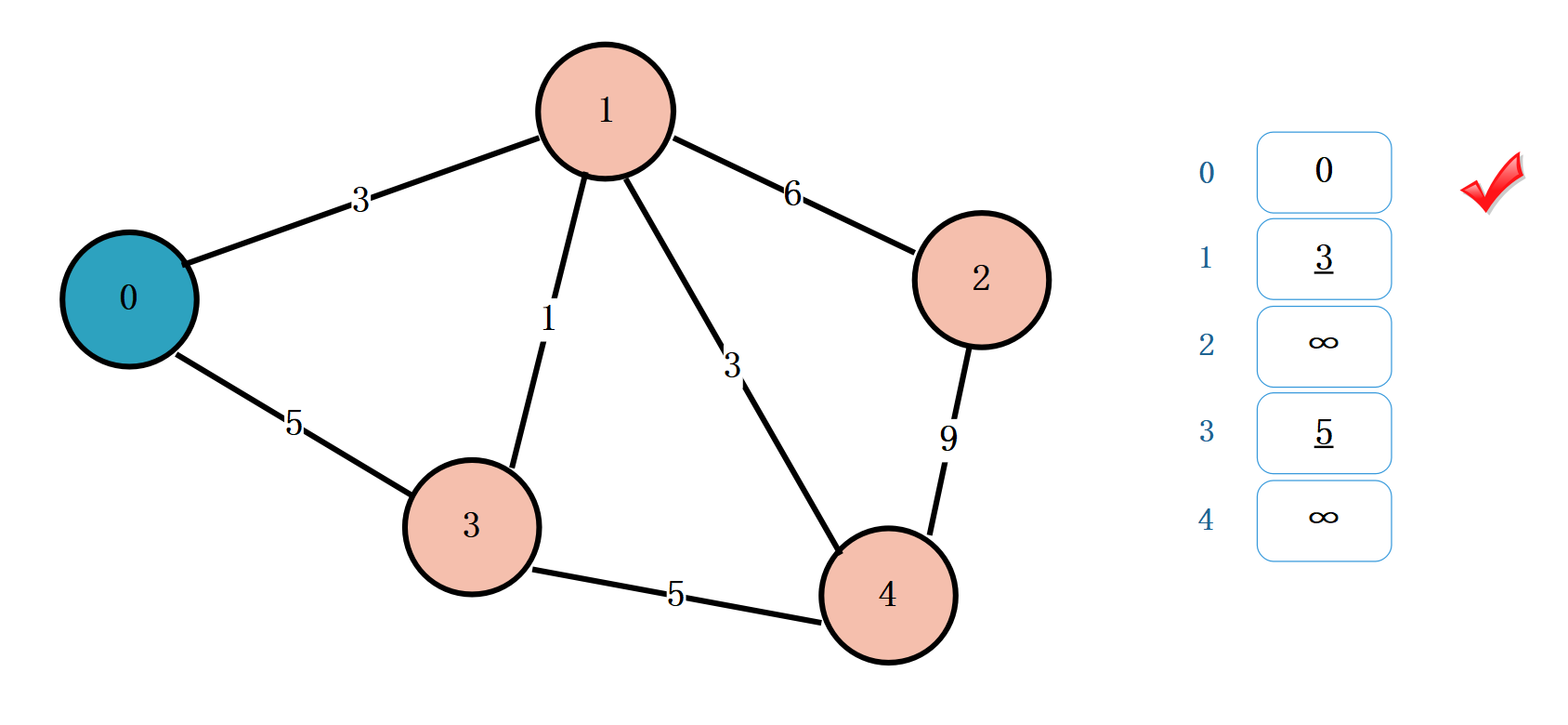
顶点 0 经过顶点 0 到达顶点 1 的距离为 3。比数组中的无穷要小。更新数组

顶点 0 经过顶点 0 到达顶点 3 的距离为 5。比数组中的无穷要小。更新数组

image-20221230203928174

从未标记的所有顶点中，找到一个距离最小的顶点，进行标记。这里的 [3，无穷，5，无穷] 中 3 最小。

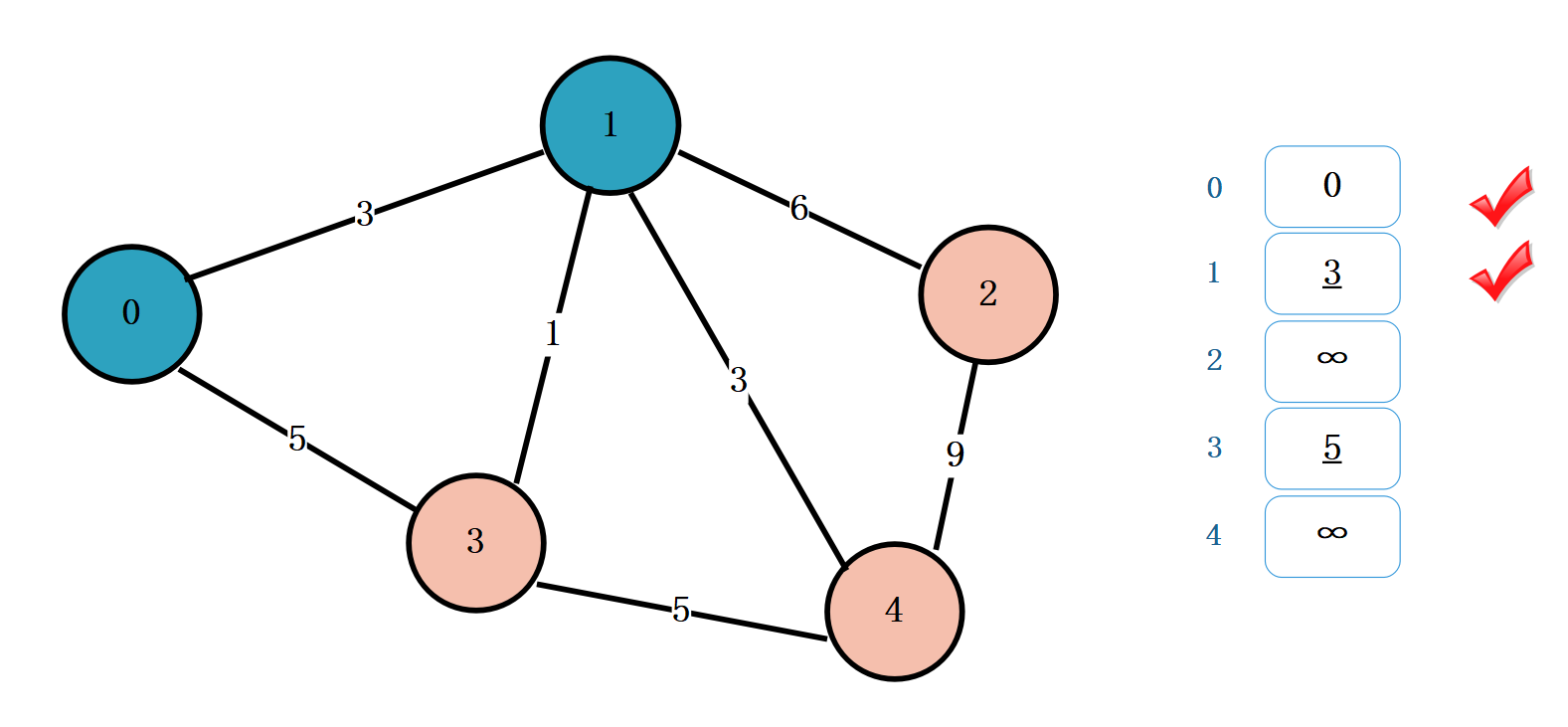
image-20221230204102979

从顶点 1 出发，找到相邻的未被标记的顶点为 3，2，4。

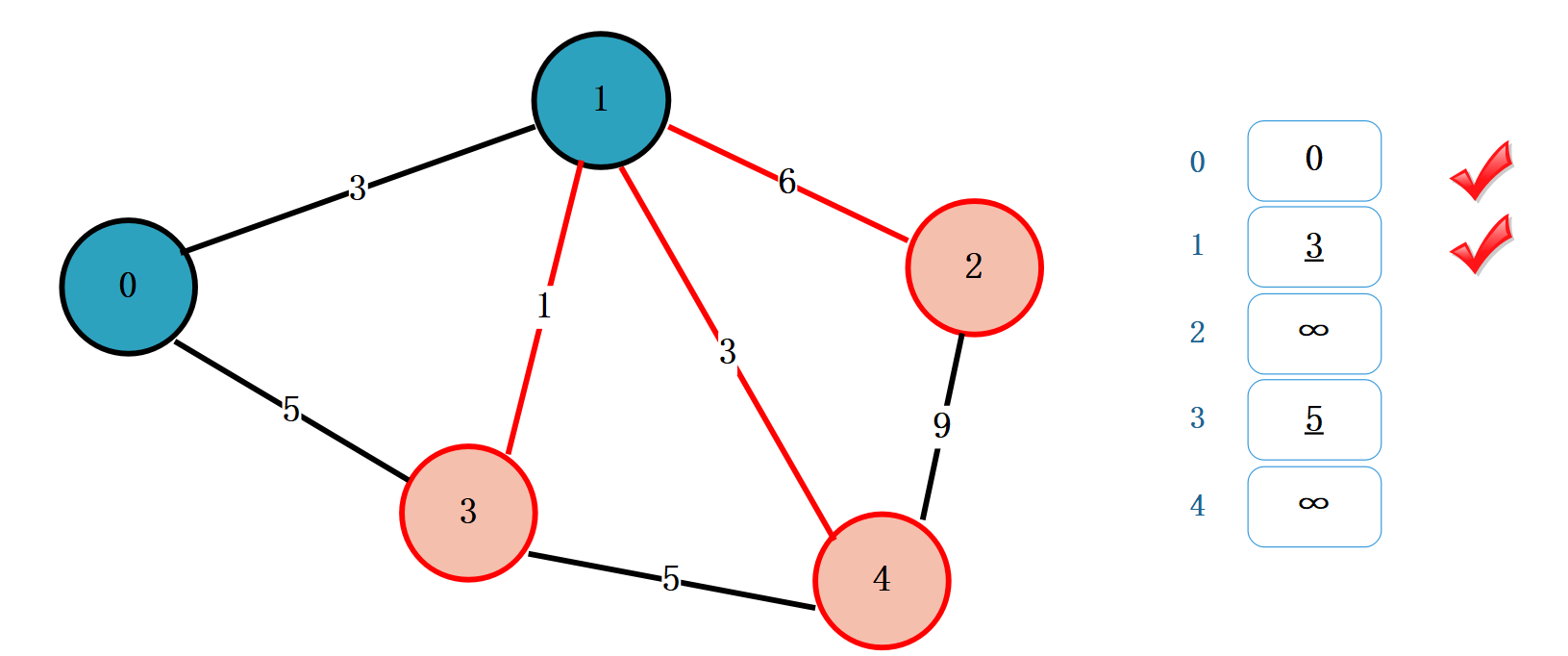
image-20221230204201055

顶点 0 经过顶点 1 到顶点 2 的最短距离为：3 + 6 = 9，比无穷小，更新数组

顶点 0 经过顶点 1 到顶点 3 的最短距离为：3 + 1 = 4， 比 5 小，更新数组

顶点 0 经过顶点 1 到顶点 4 的最短距离为：3 + 3 = 6，比无穷小，更新数组

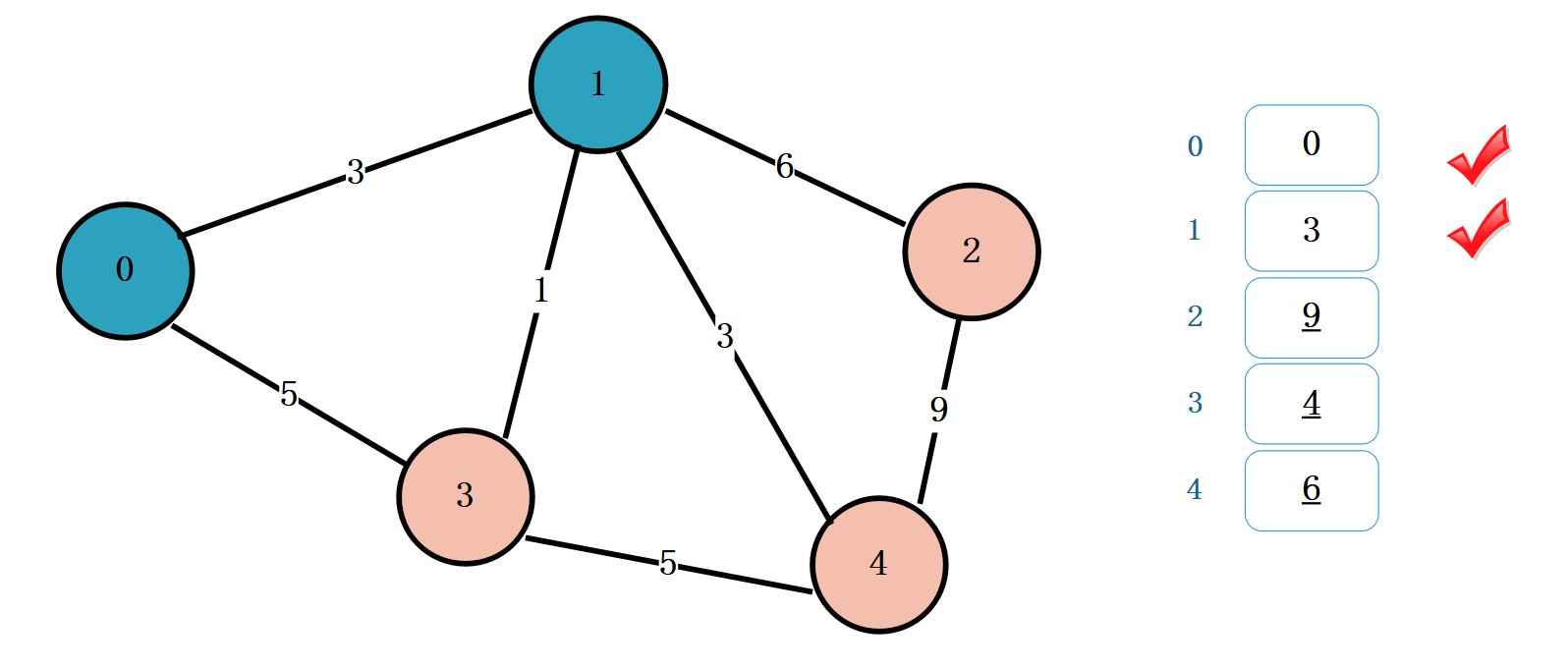
image-20221230212144512

在未标记的顶点中，找一个距离最小的。[9 , 4, 6]中 4 最小。标记顶点 3，设置 4 为顶点 0 到顶点 3 的最小距离

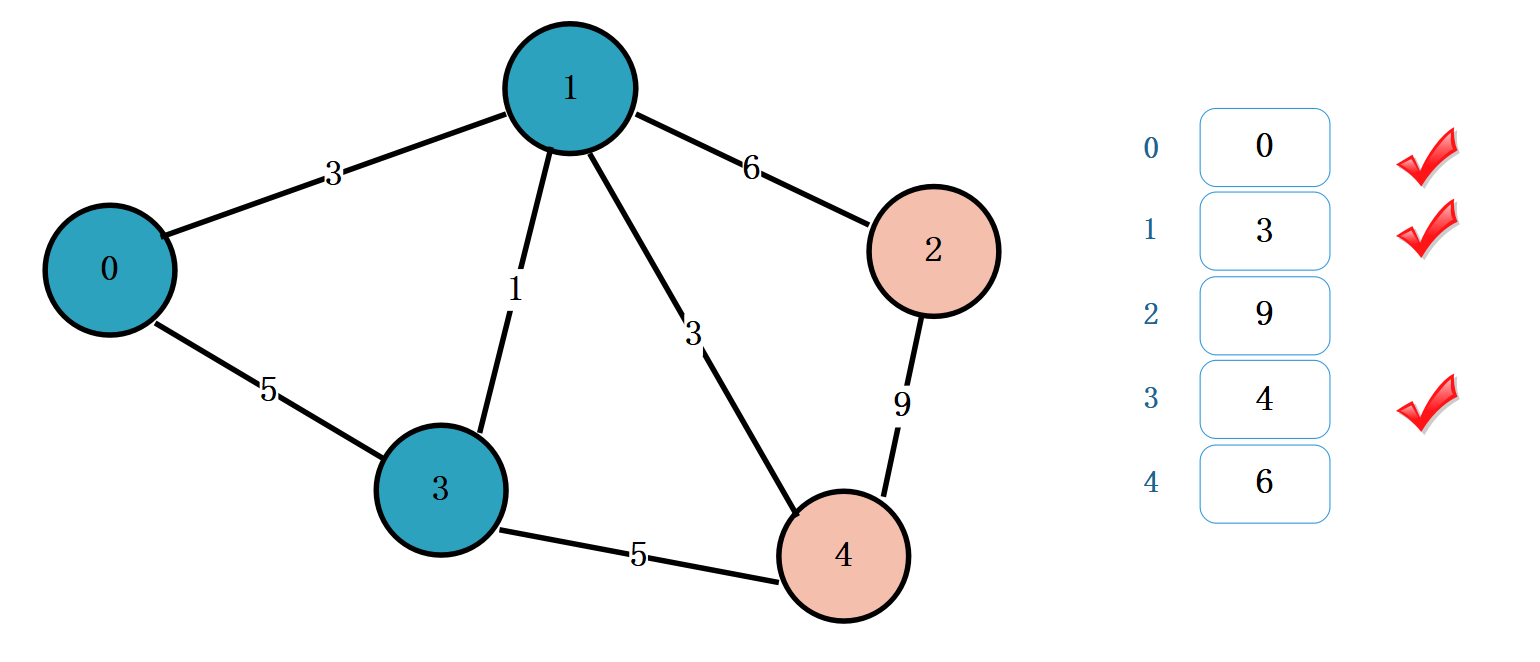
image-20221230212618407

从顶点 3 出发，找到相邻的未被标记的顶点为 4。

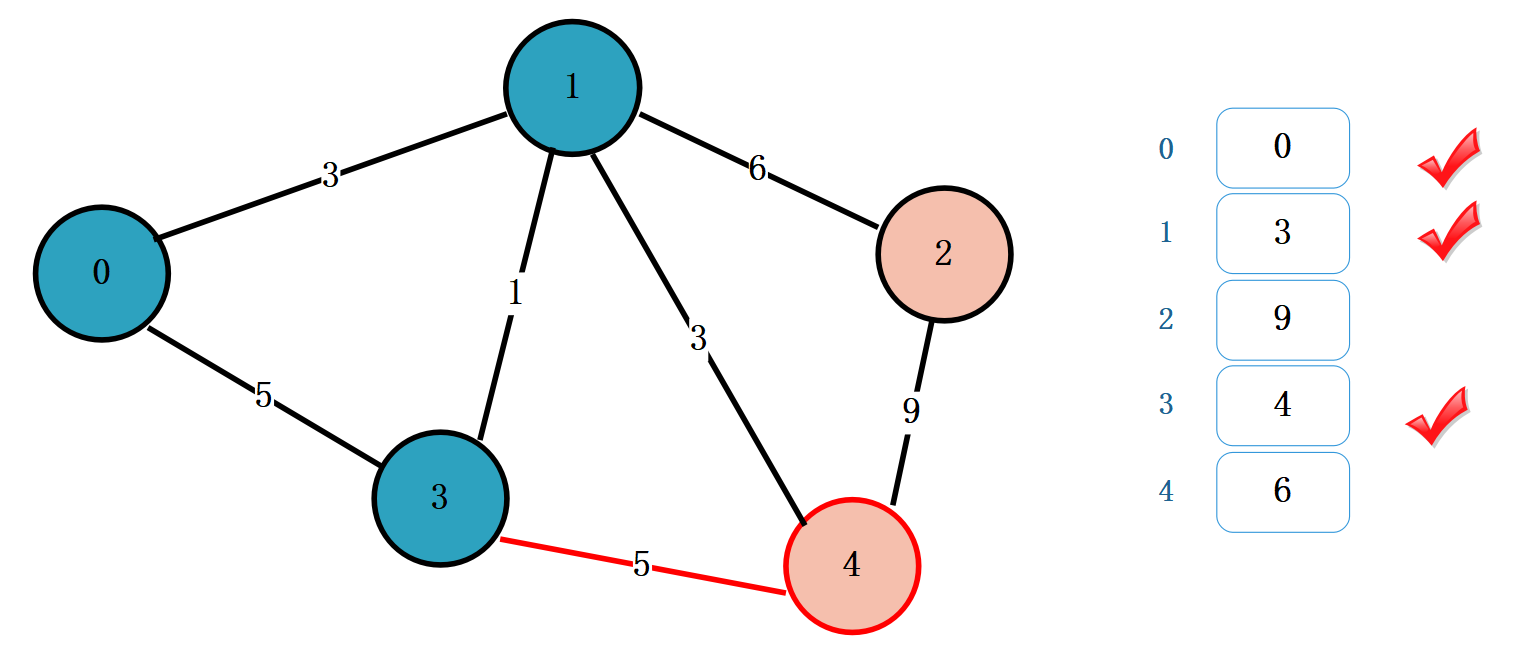
image-20221230212706071

顶点 0 经过顶点 3 到达顶点 4 的最短距离为：4 + 5 = 9，比 6 大，不用更新数组

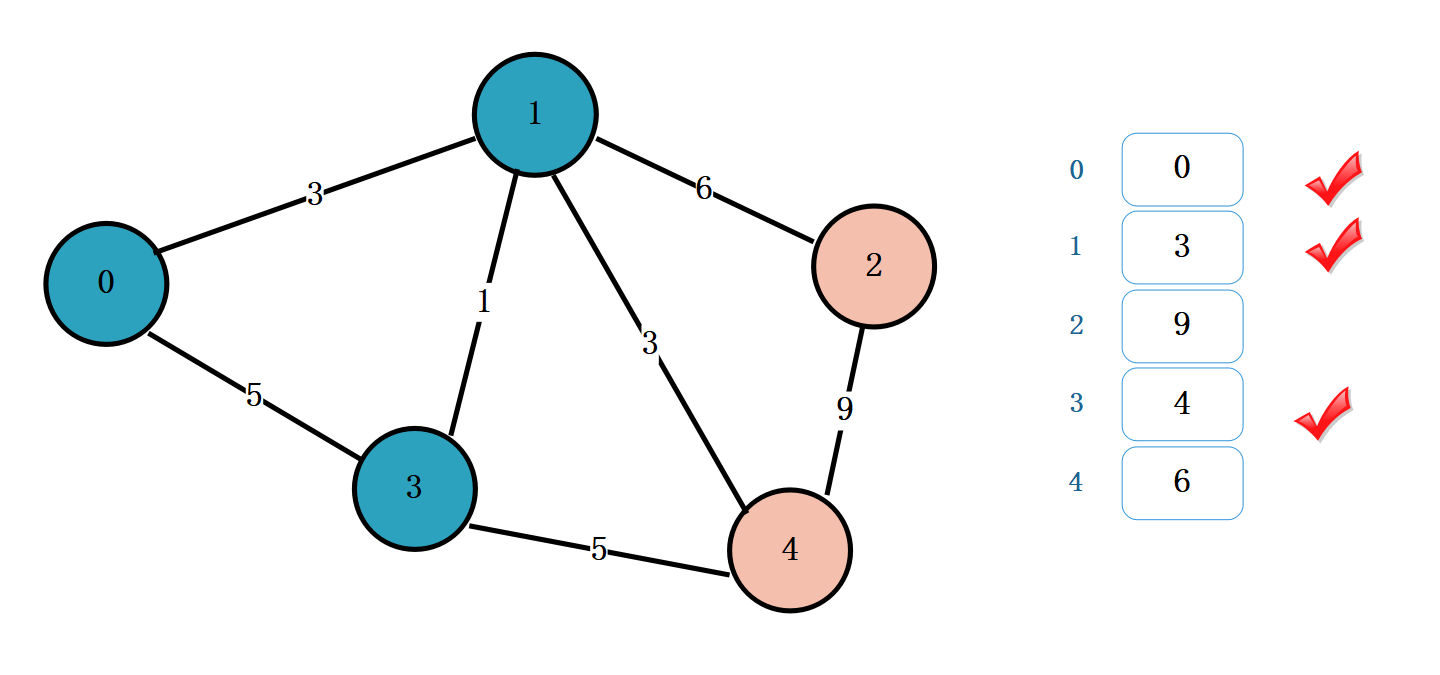
image-20221230212832384

在未标记的顶点中，找一个距离最小的。[9 , 6]中 6 最小。标记顶点 4，设置 6 为顶点 0 到顶点 4 的最小距离

image-20221230213125433

在未标记的顶点中，找一个距离最小的。这里只有一个顶点 2，将 2 标记即可

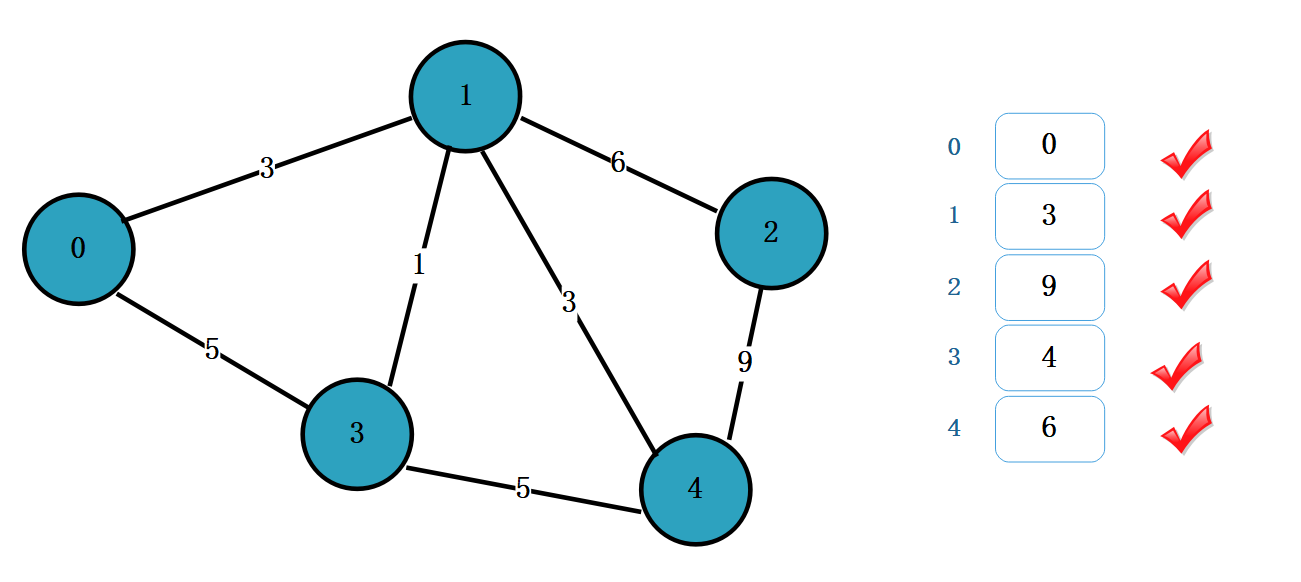
image-20221230213242139

【0，3，9，4，6】就是顶点 0 到其他顶点的最短路径

例题

743. 网络延迟时间 - 力扣（Leetcode）

有 n 个网络节点，标记为 1 到 n。

给你一个列表 times，表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi)，其中 ui 是源节点，vi 是目标节点， wi 是一个信号从源节点传递到目标节点的时间。

现在，从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1 。

示例 1：

img

1
2
输入：times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
输出：2

示例 2：

1
2
输入：times = [[1,2,1]], n = 2, k = 1
输出：1

示例 3：

1
2
输入：times = [[1,2,1]], n = 2, k = 2
输出：-1

提示：

  • 1 <= k <= n <= 100
  • 1 <= times.length <= 6000
  • times[i].length == 3
  • 1 <= ui, vi <= n
  • ui != vi
  • 0 <= wi <= 100
  • 所有 (ui, vi) 对都 互不相同（即，不含重复边）

java实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {

    public int networkDelayTime(int[][] times, int n, int k) {
        // 用数组存储边
        int[][] g = new int[n][n];
        for (int i = 0; i < g.length; i++){
            Arrays.fill(g[i], Integer.MAX_VALUE);
        }
        for (int[] t : times) {
            int x = t[0] - 1,y =  t[1] - 1;
            g[x][y] = t[2];
        }
        // 记录最小距离用的数组
        int[] dist = new int[n];
        Arrays.fill(dist, Integer.MAX_VALUE);
        // 标记点用的数组
        boolean[] flag = new boolean[n];
        dist[k - 1] = 0;
        for (int i = 0; i < n; i++) {
            // 在未标记中选择一个距离最小的进行标记
            int a = -1;
            for (int x = 0; x < n; x++) {
                if (!flag[x] && (a == -1 || dist[x] < dist[a])) {
                    a = x;
                }
            }
            flag[a] = true;
            // 从 a 出发，找相邻顶点，更新数组
            for (int x = 0; x < n; x++) {
                if (!flag[x] && g[a][x] != Integer.MAX_VALUE) {
                    dist[x] = Math.min(dist[x], dist[a] + g[a][x]);
                }
            }
        }
        int answer = Arrays.stream(dist).max().getAsInt();
        return answer == Integer.MAX_VALUE ? -1 : answer;
    }
}